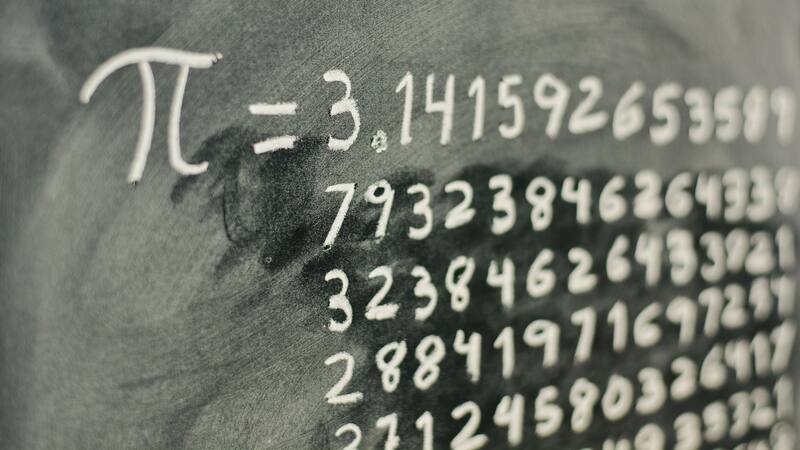
Durante siglos, la constante matemática pi () fue uno de los pilares fundamentales de la geometría, la física y la ingeniería.
Desde la antigüedad, su valor se aproximó con métodos que van desde la simple fracción 22/7 hasta complicadas series infinitas. Sin embargo, un grupo de científicos recientes desarrolló una nueva fórmula que promete simplificar cálculos complejos y ofrecer representaciones más precisas y eficientes.
Este descubrimiento podría revolucionar la forma en que entendemos las matemáticas aplicadas y abrir nuevas posibilidades en física cuántica y tecnología de punta.

La necesidad de una nueva aproximación de pi
Aunque es un número irracional, lo que significa que sus decimales se extienden infinitamente sin repetirse, los científicos siempre buscaron formas de aproximarlo con rapidez y exactitud.
La nueva fórmula surge del estudio de modelos cuánticos, donde incluso los cálculos más simples pueden requerir un poder de procesamiento enorme.
Tradicionalmente, los métodos para calcular eran demasiado lentos para aplicaciones avanzadas, como simulaciones de partículas subatómicas o desarrollo de algoritmos complejos.
La nueva aproximación permite reducir la cantidad de pasos necesarios para obtener resultados extremadamente precisos, optimizando así tanto el tiempo como los recursos computacionales.
Cómo funciona la nueva fórmula de pi
Los investigadores combinaron principios de la física de partículas con funciones matemáticas avanzadas, como la función Beta de Euler, para crear una serie convergente que se aproxima a de manera más eficiente.
La fórmula se expresa como una serie infinita que converge rápidamente, permitiendo calcular con alta precisión utilizando solo unos pocos términos. Por ejemplo, al elegir un valor específico para el parámetro, la serie puede aproximar a 10 dígitos utilizando únicamente 30 términos
A diferencia de las series tradicionales que requieren miles de términos para alcanzar una precisión alta, esta fórmula logra resultados comparables con muchos menos pasos.
Esto se traduce en cálculos más rápidos y precisos para trabajos que van desde la nanotecnología hasta simulaciones de la estructura del universo, demostrando que incluso los conceptos más abstractos de la matemática pueden tener aplicaciones prácticas en ciencia moderna.















